Demystifying the 4-Variable Karnaugh Map: A Powerful Tool for Digital Logic Design

Related Articles: Demystifying the 4-Variable Karnaugh Map: A Powerful Tool for Digital Logic Design

Introduction

In this auspicious occasion, we are delighted to delve into the intriguing topic related to Demystifying the 4-Variable Karnaugh Map: A Powerful Tool for Digital Logic Design. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the 4-Variable Karnaugh Map: A Powerful Tool for Digital Logic Design

The realm of digital logic design thrives on the ability to manipulate and represent Boolean expressions efficiently. One of the most effective tools for this purpose is the Karnaugh map (K-map), a graphical representation that simplifies the process of minimizing Boolean expressions. While K-maps exist for various numbers of variables, the 4-variable K-map stands out as a versatile and practical tool used extensively in digital circuit design and analysis.

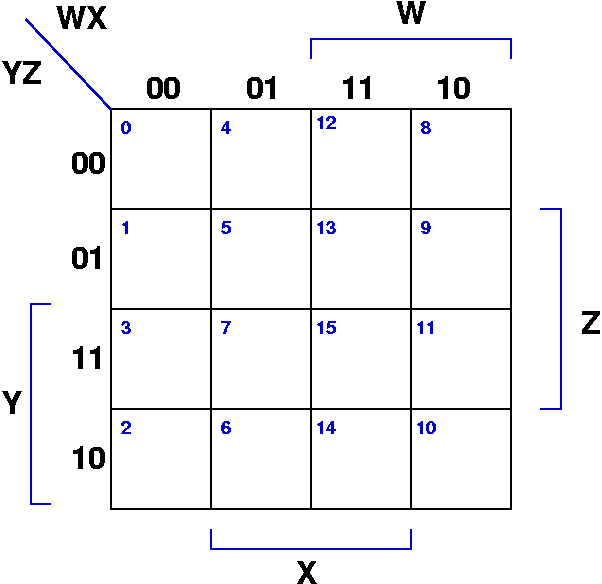
Understanding the Basics: Constructing a 4-Variable K-Map

A 4-variable K-map is a two-dimensional grid composed of 16 cells, each representing a unique combination of the four input variables. These variables, typically denoted as A, B, C, and D, are assigned binary values (0 or 1) to represent the state of the inputs. The arrangement of the cells within the K-map is crucial for its effectiveness:

• Rows and Columns: The rows of the K-map represent the values of two variables, usually A and B. The columns represent the values of the remaining two variables, typically C and D.
• Gray Code Ordering: The order of the rows and columns follows a Gray code sequence. Gray code ensures that only one bit changes between adjacent cells, facilitating the identification of adjacent groups of 1s.

The Power of Adjacency: Simplifying Boolean Expressions

The true power of the K-map lies in its ability to visually represent and simplify Boolean expressions. The simplification process hinges on the concept of adjacency:

• Adjacent Cells: Cells in a K-map are considered adjacent if they share a common edge, even if they appear to be separated by a boundary. This includes cells at the extreme ends of rows and columns, which are considered adjacent.
• Grouping 1s: The goal is to group together adjacent cells containing a "1" (representing a true output). These groups must be rectangular and contain a power of two number of cells (1, 2, 4, 8).
• Minimization: Each group represents a simplified product term (AND operation) in the final Boolean expression. The variables that remain constant within a group are included in the product term, while the variables that change are excluded.

Illustrative Example: A Practical Demonstration

Let’s consider a Boolean expression:

F(A, B, C, D) = Σ(0, 2, 4, 6, 8, 10, 12, 14)

This expression represents a function with eight minterms, each corresponding to a specific combination of input values. To simplify this expression using a K-map:

1. Construct the K-map: Create a 4-variable K-map and place a "1" in the cells corresponding to the minterms listed in the expression.

2. Identify Groups: Encircle the largest possible groups of adjacent "1"s, ensuring each group contains a power of two number of cells.

3. Write the Simplified Expression: For each group, identify the variables that remain constant within the group and form a product term (AND operation). The final simplified expression is the sum (OR operation) of these product terms.

Benefits of Using 4-Variable K-maps

The 4-variable K-map offers numerous advantages for digital logic design:

• Visual Representation: The graphical nature of the K-map allows for a clear and intuitive visualization of the Boolean expression, making it easier to identify patterns and simplify the expression.
• Simplification: K-maps provide a systematic and efficient method for minimizing Boolean expressions, resulting in simpler and more cost-effective digital circuits.
• Reduced Complexity: K-maps eliminate the need for complex algebraic manipulations, simplifying the design process and reducing the chances of errors.
• Improved Performance: Simplified circuits typically consume less power and operate faster, leading to improved overall performance.

FAQs on 4-Variable K-Maps

1. What happens if there are no adjacent 1s in the K-map?

If there are no adjacent 1s, each "1" represents a unique minterm, and the simplified expression will be the sum of these individual minterms.

2. What if there are multiple ways to group 1s in a K-map?

In such cases, choose the grouping that results in the fewest product terms and the simplest overall expression.

3. Can K-maps be used for functions with more than four variables?

While 4-variable K-maps are commonly used, they can be extended to handle functions with more variables. However, the complexity of the map increases significantly with each additional variable.

4. What are some common applications of 4-variable K-maps?

4-variable K-maps are widely used in designing digital circuits, including:

• Logic gates: Implementing AND, OR, NOT, XOR, and other logic gates.
• Combinational circuits: Designing adders, subtractors, decoders, and encoders.
• Sequential circuits: Analyzing and simplifying state machines.

Tips for Using 4-Variable K-Maps Effectively

• Start with the largest groups: Prioritize grouping the largest possible number of adjacent 1s to achieve maximum simplification.
• Use Gray code ordering: Ensure the rows and columns are arranged in Gray code to facilitate the identification of adjacent cells.
• Don’t forget the wrap-around: Remember that cells at the extreme ends of rows and columns are considered adjacent.
• Practice makes perfect: The more you use K-maps, the more proficient you will become at identifying groups and simplifying expressions.

Conclusion: The Enduring Value of K-maps

The 4-variable K-map remains a valuable tool for digital logic designers, offering a visual and intuitive approach to simplifying Boolean expressions. Its effectiveness in minimizing circuits, reducing complexity, and improving performance makes it an essential component in the design and analysis of digital systems. While more advanced tools and techniques exist, the K-map continues to provide a fundamental understanding of Boolean logic and its applications in digital circuit design.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the 4-Variable Karnaugh Map: A Powerful Tool for Digital Logic Design. We hope you find this article informative and beneficial. See you in our next article!